Turinys

• Žingsniai
• 1 iš 3 metodas: 1 dalis. Lūžio taško nustatymas
• 2 metodas iš 3: funkcijos išvestinių priemonių apskaičiavimas
• 3 metodas iš 3: 3 dalis. Raskite lenkimo tašką
• Patarimai

Diferencialiniame skaičiavime lenkimo taškas yra kreivės taškas, kuriame jo kreivumas keičia ženklą (iš pliuso į minusą arba iš minuso į pliusą). Ši koncepcija naudojama mechaninėje inžinerijoje, ekonomikoje ir statistikoje, siekiant nustatyti reikšmingus duomenų pokyčius.

Žingsniai

1 iš 3 metodas: 1 dalis. Lūžio taško nustatymas

1. 1 Įgaubtos funkcijos apibrėžimas. Bet kurios akordo vidurys (segmentas, jungiantis du taškus) įgaubtos funkcijos grafike yra po grafiku arba ant jo.
2. 2 Išgaubtos funkcijos apibrėžimas. Bet kurios akordo vidurys (segmentas, jungiantis du taškus) išgaubtos funkcijos grafike yra virš grafiko arba ant jo.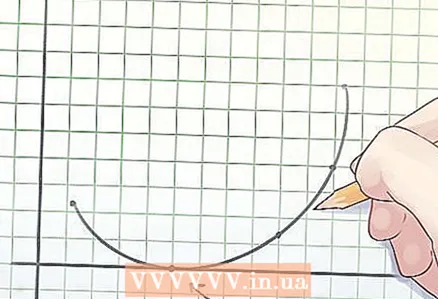
3. 3 Funkcijos šaknų nustatymas. Funkcijos šaknis yra kintamojo „x“ vertė, prie kurios y = 0.
   • Nubraižant funkciją, šaknys yra taškai, kuriuose grafikas kerta x ašį.

2 metodas iš 3: funkcijos išvestinių priemonių apskaičiavimas

1. 1 Raskite pirmąjį funkcijos darinį. Pažvelkite į vadovėlio diferenciacijos taisykles; turite išmokti imtis pirmųjų išvestinių priemonių ir tik tada pereiti prie sudėtingesnių skaičiavimų. Pirmieji dariniai žymimi f '(x). Formos ax ^ p + bx ^ (p - 1) + cx + d išraiškoms pirmasis darinys yra: apx ^ (p - 1) + b (p - 1) x ^ (p - 2) + c.
   • Pavyzdžiui, raskite funkcijos f (x) = x ^ 3 + 2x -1 linksniuotės taškus. Pirmasis šios funkcijos darinys yra:
     
     f ′ (x) = (x ^ 3 + 2x - 1) ′ = (x ^ 3) ′ + (2x) ′ - (1) ′ = 3x ^ 2 + 2 + 0 = 3x2 + 2
2. 2 Raskite antrąją funkcijos išvestinę. Antrasis darinys yra pirminės funkcijos pirmojo išvestinio darinio darinys. Antrasis darinys žymimas kaip f ′ ′ (x).
   • Pirmiau pateiktame pavyzdyje antrasis darinys yra:
     
     f ′ ′ (x) = (3x2 + 2) ′ = 2 × 3 × x + 0 = 6x
3. 3 Nustatykite antrąją išvestinę nulį ir išspręskite gautą lygtį. Rezultatas bus tikėtinas posūkio taškas.
   • Aukščiau pateiktame pavyzdyje jūsų skaičiavimas atrodo taip:
     
     f ′ ′ (x) = 0
     6x = 0
     x = 0
4. 4 Raskite trečiąjį funkcijos darinį. Norėdami patikrinti, ar jūsų rezultatas iš tikrųjų yra posūkio taškas, raskite trečiąją išvestinę priemonę, kuri yra pirminės funkcijos antrosios išvestinės išvestinė. Trečioji išvestinė žymima kaip f ′ ′ (x).
   • Pirmiau pateiktame pavyzdyje trečioji išvestinė yra:
     
     f ′ ′ (x) = (6x) ′ = 6

3 metodas iš 3: 3 dalis. Raskite lenkimo tašką

1. 1 Patikrinkite trečiąją išvestinę. Standartinė linksniuojamojo taško įvertinimo taisyklė yra ta, kad jei trečioji išvestinė nėra lygi nuliui (tai yra, f ′ ′ (x) ≠ 0), tai linksniuotės taškas yra tikrasis posūkio taškas. Patikrinkite trečiąją išvestinę priemonę; jei jis nėra nulis, tada radote tikrąjį posūkio tašką.
   • Pirmiau pateiktame pavyzdyje trečioji išvestinė yra 6, o ne 0.Taigi jūs radote tikrąjį posūkio tašką.
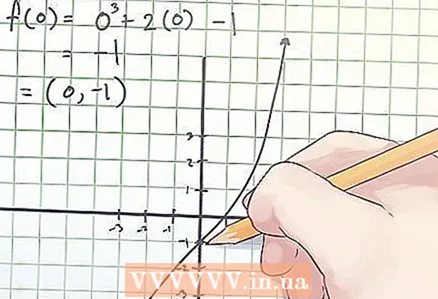2. 2 Raskite posūkio taško koordinates. Linkimo taško koordinatės žymimos kaip (x, f (x)), kur x yra nepriklausomo kintamojo „x“ reikšmė linksniuotės taške, f (x) yra priklausomo kintamojo „y“ vertė posūkio metu taškas.
   • Anksčiau pateiktame pavyzdyje, prilygindami antrąją išvestinę nuliui, nustatėte, kad x = 0. Taigi, norėdami nustatyti linksnio taško koordinates, raskite f (0). Jūsų skaičiavimas atrodo taip:
     
     f (0) = 0 ^ 3 + 2 × 0−1 = −1.
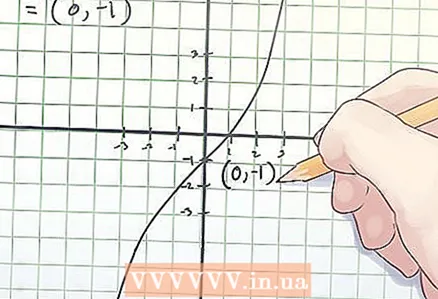3. 3 Užsirašykite lankstymo taško koordinates. Linksnių taškų koordinatės yra rastos x ir f (x) vertės.
   • Anksčiau pateiktame pavyzdyje posūkio taškas yra koordinatėse (0, -1).

Patarimai

• Pirmoji laisvojo termino išvestinė (pirminis skaičius) visada lygi nuliui.